
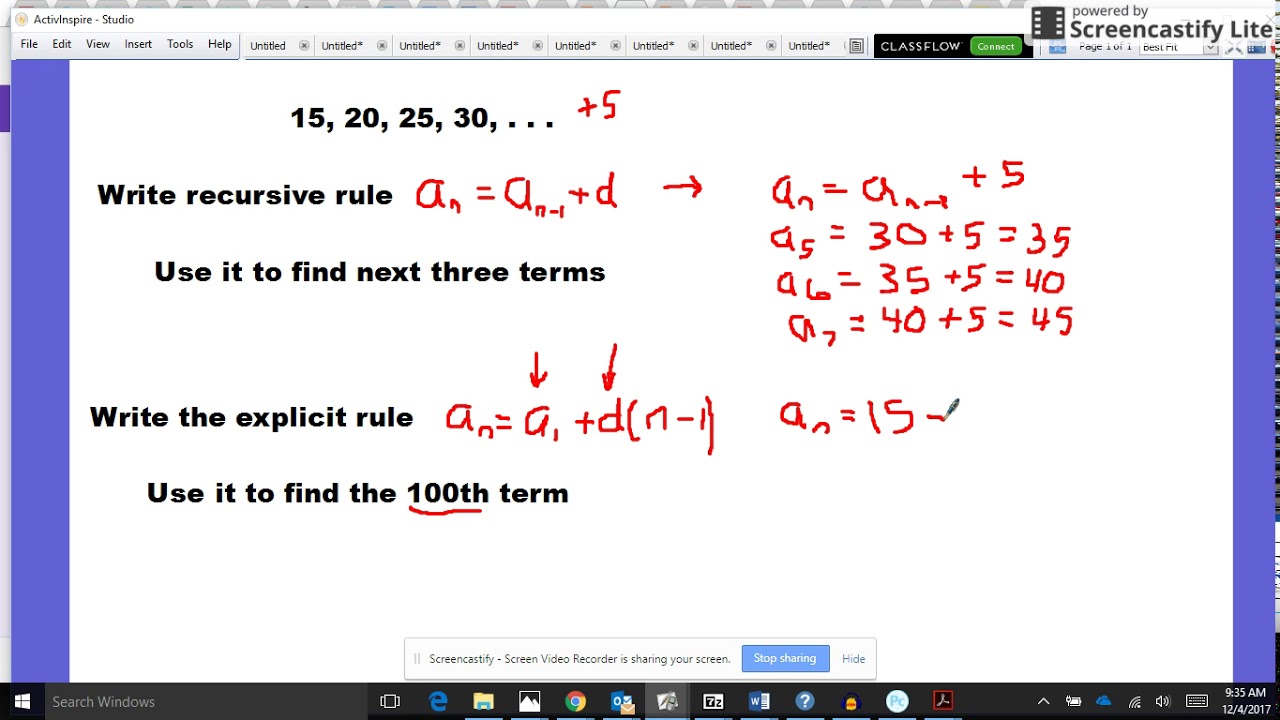
Now we can find it's roots which are $\frac\right)^n$$Īnd that would be a closed form formula for the Fibonacci numbers and you could use this method. It comes from the same root as the word recur, and is a technique that involves repeatedly applying a self-referencing definition until we reach some initial terms that are explicitly defined, and then going back through the. First of all let's use the characteristic polynomial of the definition which is $x^2-x-1$ (we got it by assuming the solution is of the form $a_n=\lambda n.n^c$ and moving sides, because you can get all the solutions using a linear combination of 2 solutions then we can just use these 2 solutions to find the rest). You may be familiar with the term recursion as a programming technique. The explicit showing of how the practices she is describing are manifested in every element of these concrete sequences adds to the credibility of her. Arithmetic Sequences Definition, Explicit & Recursive Formulas. Converting recursive & explicit forms of arithmetic sequences You might need: Calculator fn93+4n-1 Complete the recursive formula of fn. But I guess you want the Fibonacci sequence so the starting conditions will be $a_0=a_1=1$.

You can't have an explicit formula without starting conditions. This Khan Academy: Converting Recursive and Explicit Forms of Arithmetic Sequences Unknown Type is suitable for 9th - 10th Grade.


 0 kommentar(er)
0 kommentar(er)
